Number theory has always interested me, specifically irrational numbers and prime numbers. I was messing around with functions in R and came up with a very neat ‘one line’ function in R that checks if a number is prime. See below:
IsPrime = function(n){if(n>3){if(any(sapply(seq(2,floor(sqrt(n))),function(x) n%%x)==0)){FALSE}else{TRUE}}else if (n%in%c(2,3)){TRUE} else{FALSE}}
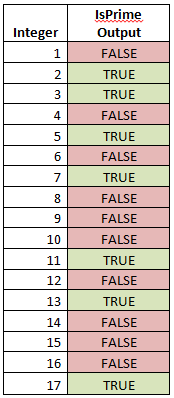
(Bonus Math Karma to anyone that knows why the square root function is in there). To check the function works, here are the first 17 integers checked:
Looks good so far. This ‘IsPrime’ function checks integers for being prime. I thought to myself, what are the reaches of this function? How big of a number can I check with reasonable times/resources? Let’s create a sequence of very large numbers.
prime.seq.check = 10^(seq(5,14))+1
Note that the vector ‘prime.seq.check’ contains the sequence:
100,001; 1,000,001; 10,000,001; …
And so on, and ends with a 15 digit integer:
100,000,000,000,001 (A hundred billion and one). What are the times to compute if these are prime? Let’s use the ‘proc.time’ R-function to loop through and time these.
times = rep(0,length(prime.seq.check))
prime.log = rep(0,length(prime.seq.check))
for (p in 1:length(prime.seq.check)){
tic = proc.time()[3]
prime.log[p] = IsPrime(prime.seq.check[p])
times[p] = proc.time()[3]-tic
print(paste("Done with ",p," out of ",length(prime.seq.check),sep=""))
}
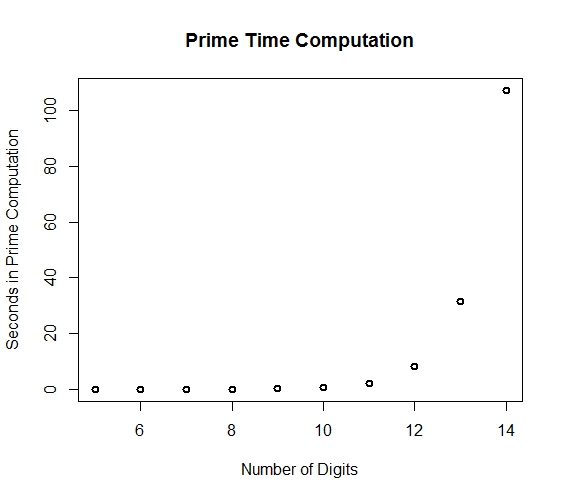
Let’s plot the output:
plot(seq(5,14),times,main="Prime Time Computation", xlab="Number of Digits",
ylab="Seconds in Prime Computation",lwd=2)
Looks very exponential. Let’s fit an exponential function using some basic algebra.
x.seq = seq(0,14,by=0.1)
y1 = times[10]
x1 = 14
y2 = times[9]
x2 = 13
b = (log(y1/y2))/(x1-x2)
c = y1/(exp(b*x1))
y.seq = (c)*exp((b)*x.seq)
plot(seq(5,14),times,main="Prime Time Computation", xlab="Number of Digits",
ylab="Seconds in Prime Computation",lwd=2)
grid()
lines(x.seq,y.seq,col="red",lwd=2)
points(seq(5,14),times,lwd=2)
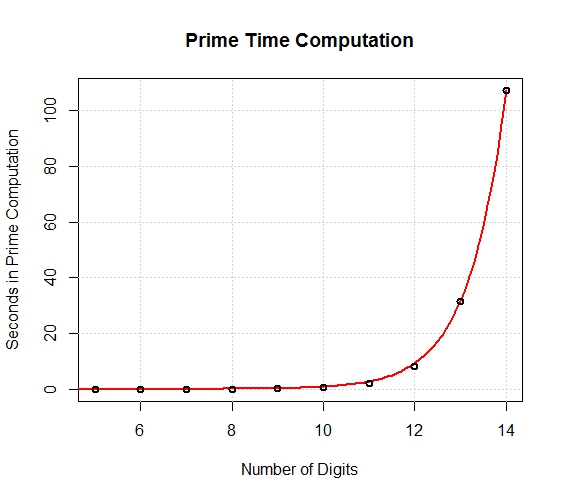Turns out the function is given by f(x) = (4.082583E-6) * exp(1.220295 * x). The largest prime to date has 17,425,170 digits. I used Wolfram Alpha to calculate this, and it would take about 2E9234766 seconds. MUCH longer than the estimated age of the universe.
So, needless to say, this prime number function is not going to help in the search for prime numbers. But it is cool.
More props to you, pure math.